Remote sensing offers spatially and temporally continuous measurements of hydrological fluxes like rainfall, evapotranspiration, and soil moisture. These measurements provide valuable information in data-scarce catchments around the world. Nevertheless, owing to a variety of sensor and retrieval algorithms, remote sensing data is subject to large uncertainties and errors. Therefore, it is imperative that remote sensing datasets are rigorously validated using ground truth before such datasets are used for applications such as calibration of climate forecasts, hydrologic modeling, and streamflow forecasting.
As an example, we can compare and validate different remotely sensed precipitation datasets using ground-based measurements for a catchment in East Africa. The area of study is the Omo-Gibe river basin in Ethiopia, using a time period of at least 1 year.
The comparison should focus on:
- Description of catchment climatology using publicly available precipitation datasets
- Preprocessing of these datasets (NetCDF format)
- Comparison of different datasets and
- Validation of these datasets (both spatial and non-spatial).
Preprocessing of Data
First, clear your workspace, set your working directory, and load the required library
# clear workspace
rm(list=ls())
#set working directory
setwd("/home/username/Downloads/Scripts/...")
#load required library
library(raster)Next, download and preprocess remotely sensed rainfall datasets for the study area.
# load precipitation data
Centrends = brick("CenTrends_v1_monthly.nc",varname = "precip") GPCC=brick("precip.mon.total.v7.nc")
TRMM =brick("prcp_trmm_2004.nc")
# Load Omogibe shapefile
gibe_shp = shapefile("omogibe.shp")
# extract only 2004 data from centrends and gpcc
dates_Centrends = names(Centrends)
dates_GPCC = names(GPCC)
# find year 2004
index_Centrends= grep("2004" ,dates_Centrends)
index_GPCC = grep("2004" ,dates_GPCC)
# subset the data to 2004
Centrends = Centrends[[index_Centrends]]
GPCC = GPCC[[index_GPCC]]
# fix the coordinates of GPCC and TRMM
# rotate gpcc and trmm data, but centrends is correct(no need to rotate)
GPCC = rotate(GPCC)
TRMM = rotate(TRMM)
# crop the datasets to Omogibe catchment
centrends_gibe = crop(Centrends,gibe_shp)
gpcc_gibe = crop(GPCC,gibe_shp)
trmm_gibe = crop(TRMM,gibe_shp)The datasets include TRMM 3B42RT, CMORPH, PERSIANN, and CenTrends (Ground truth data). Ground truth data (Centrends long-term rainfall record) should be used to quantify the climatology of the study area. Seasonality, inter-annual variability, and long-term change in rainfall in the study area should be adequately described.
Comparison of Remote Sensing Datasets
Next, we can complete a comprehensive comparison of the processed rainfall datasets including basin-averaged values and spatial distribution of rainfall in the study catchment for different seasons.
#extract mean value from the 3 datasets
centrends_avg = extract(centrends_gibe,gibe_shp,mean,na.rm=TRUE)
gpcc_avg = extract(gpcc_gibe,gibe_shp,mean,na.rm=TRUE)
trmm_avg = extract(trmm_gibe,gibe_shp,mean,na.rm=TRUE)
# create dataframe of mean values
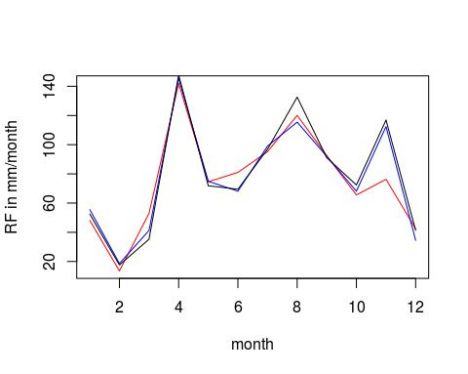
data_mean = data.frame(Centrends = c(centrends_avg), GPCC = c(gpcc_avg), TRMM = c(trmm_avg)) # create a plot of the 3 precipitation data
plot(c(1:12) ,data_mean[ ,"Centrends"],type="l" ,xlab="month" ,ylab="RF in mm/month" ,col="red") lines(data_mean[,"TRMM"],col="blue")
lines(data_mean[,"GPCC"],col="black")
# Comparing raster data (spatially)
# equalize the resolution of the datasets
centrends_gibe = projectRaster(centrends_gibe,trmm_gibe)
gpcc_gibe = projectRaster(gpcc_gibe,trmm_gibe)
# plot three rasters together
# 1=row, 3=columns
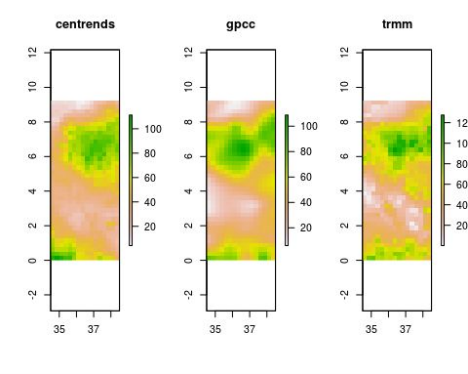
par(mfrow = c(1,3))
plot(centrends_gibe[[1]])
title("centrends")
plot(gpcc_gibe[[1]])
title("gpcc")
plot(trmm_gibe[[1]])
title("trmm")Evaluation of Remote Sensing Datasets
We can calculate relevant error metrics to compare and select the best remote-sensing datasets. While there are many different error metrics, an important one to include is RMSE. Error metrics should be calculated for basin averages and each grid pixel to characterize the spatial distribution of error.
# calculation of RMSE error
GT = data_mean[,"Centrends"] #ground truth
RS = data_mean[,"TRMM"] #remote sensing data
# RMSE
rmse=sqrt(mean((GT-RS)^2))
# calculation of MAE
mae=mean(abs(GT-RS))
# correlation(values varies b/n 1 and -1)
correlation=cor(GT,RS)
# calculation of spatial errors
gt = centrends_gibe
rs = trmm_gibe
# step 1 calculate the dif erence b/n GT and RS data
diff_raster=gt-rs
# step 2 calculate the square of the dif erence
square_raster=(gt-rs)^2
# step 3 calculate the mean
mean_raster=stackApply(square_raster,c(1,1,1,1,1,1,1,1,1,1,1,1),mean,na.rm = TRUE) # step4 calculate rmse for each pixel
rmse_raster=sqrt(mean_raster)
# calculation of of spatial MAE
diff_raster=gt-rs
abs_raster = abs(diff_raster)
mae_raster=stackApply(abs_raster,c(1,1,1,1,1,1,1,1,1,1,1,1),mean,na.rm = TRUE)Output
# print data and values
centrends_avg
# X2004.01.30 X2004.03.01 X2004.03.30 X2004.04.30 X2004.05.30 X2004.06.30 X2004.07.30 [1,] 48.15352 13.57746 52.95584 141.9959 74.6393 81.02153 95.22529 X2004.08.30 X2004.09.30 X2004.10.30 X2004.11.30 X2004.12.30 [1,] 120.071 92.46025 65.59274 76.29582 42.3984
gpcc_avg
# X2004.01.01 X2004.02.01 X2004.03.01 X2004.04.01 X2004.05.01 X2004.06.01 X2004.07.01 [1,] 52.5218 17.6262 35.2628 147.755 71.842 69.488 96.9292 X2004.08.01 X2004.09.01 X2004.10.01 X2004.11.01 X2004.12.01 [1,] 132.5842 91.0448 72.4016 116.918 41.3116
trmm_avg
# X2004.01.16 X2004.02.15 X2004.03.16 X2004.04.15 X2004.05.16 X2004.06.15 X2004.07.16[1,] 55.5454 18.6204 41.24854 145.4656 74.89386 68.13789 99.03134 X2004.08.16 X2004.09.15 X2004.10.16 X2004.11.15 X2004.12.16 [1,] 115.4681 91.98316 68.13575 112.3921 34.48828
The above results can be summarized in a table and further examined.
- correlation = 0.9402921
- mae = 8.015455
- rmse = 12.25799
| index | index_Centrends | index_GPCC | GT | RS |
|---|---|---|---|---|
| 1 | 1249 | 1237 | 48.15352 | 55.5454 |
| 2 | 1250 | 1238 | 13.57746 | 18.6204 |
| 3 | 1251 | 1239 | 52.95584 | 41.24854 |
| 4 | 1252 | 1240 | 141.99591 | 145.46563 |
| 5 | 1253 | 1241 | 74.6393 | 74.89386 |
| 6 | 1254 | 1242 | 81.02153 | 68.13789 |
| 7 | 1255 | 1243 | 95.22529 | 99.03134 |
| 8 | 1256 | 1244 | 120.07101 | 115.46809 |
| 9 | 1257 | 1245 | 92.46025 | 91.98316 |
| 10 | 1258 | 1246 | 65.59274 | 68.13575 |
| 11 | 1259 | 1247 | 76.29582 | 112.39205 |
| 12 | 1260 | 1248 | 42.3984 | 34.48828 |